HMAC vs. RSA vs. ECDSA: Which algorithm should you use to sign JWTs?

One of the most common ways to authenticate and authorize users in modern web applications is through JSON Web Tokens (JWTs). These tokens ensure that the data transmitted between the server and client remains tamper-proof and that the user is properly authenticated. However, securing JWTs requires a solid understanding of cryptographic techniques, particularly algorithms for signing and verifying these tokens.

Two of the most commonly used cryptographic algorithms for securing JWTs are HMAC (Hash-based Message Authentication Code) and RSA (Rivest-Shamir-Adleman). Each of these algorithms has its strengths and weaknesses, and choosing the right one can make a significant difference in terms of performance and security. But there’s also another contender on the horizon — ECDSA (Elliptic Curve Digital Signature Algorithm), which many experts argue is the future of cryptographic security.

In this article, we’ll explore HMAC, RSA, and ECDSA, explain how they work, when to use each of them, and how they are applied in the context of JWT. By the end of this article, you should have a clear understanding of these algorithms and be able to make an informed decision about which one to use for your own app.

JWT 101

Before diving into cryptographic algorithms, let’s first understand what JWTs are and why they’re important.

A JSON Web Token (JWT) is a compact, URL-safe token used for securely transmitting information between two parties. Typically, JWTs are used for authentication purposes, allowing a server to verify the identity of a user without needing to store session information.

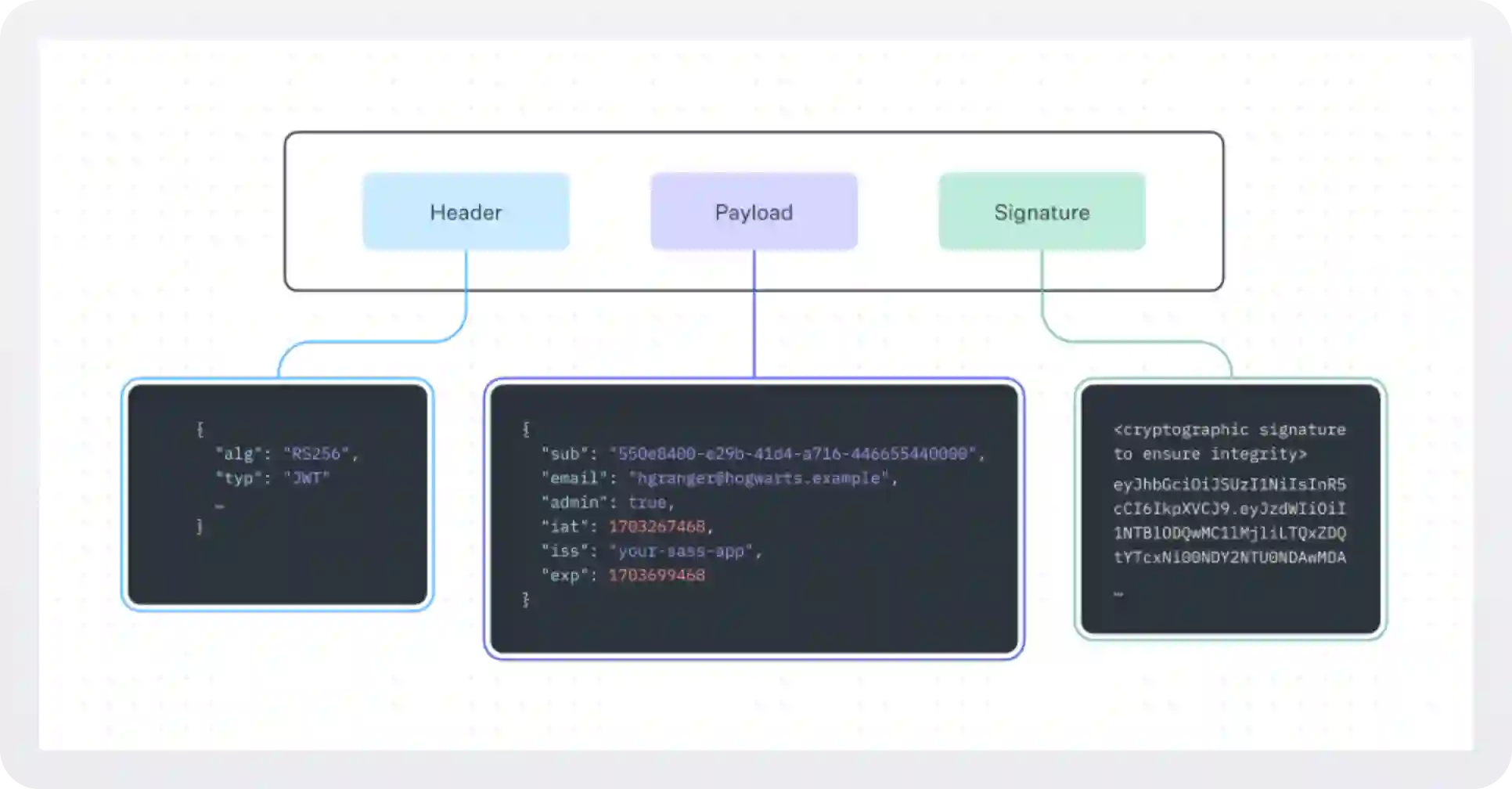
A JWT consists of three parts: the header, the payload, and the signature:

• The header typically specifies the algorithm used to sign the token (e.g., HMAC, RSA, or ECDSA) and the type of token.
• The payload contains the claims or the data — such as user ID, roles, or permissions — that the token is encoding.
• The signature is the most critical part, ensuring the integrity of the token and confirming that it was issued by a trusted source.

JWTs are protected via JSON Web Signature (JWS). JWS uses a signature algorithm and is used to share data between parties when confidentiality is not required. This is because claims within a JWS can be read as they are simply base64-encoded (but carry with them a signature for authentication).Some of the cryptographic algorithms JWS uses are HMAC, RSA, and ECDSA.

JWT signing

When an app receives a JWT, it has to verify whether it’s legitimate. This is where signing comes into play. Signing a JWT guarantees that the data inside it hasn’t been tampered with and that it comes from a trusted source. Each signature is unique based on the token’s contents, which helps prevent anyone from modifying the token without being detected.

Different algorithms can be used to sign a JWT. Which one you use determines both the security level and the computational efficiency of the JWT.

JWT signing algorithms can be classified into two categories: symmetric and asymmetric.

• Symmetric algorithms use the same secret key to sign and verify the tokens. They are faster and simpler but require secure key distribution because all parties need the same key. This makes them unsuitable for apps that require high security and scalability, like distributed systems or multi-tenant applications.
• Asymmetric algorithms use a pair of public and private keys to sign and verify the tokens. They are more secure, scalable, and better for secure, distributed systems, but they are also more resource-intensive and complex.

The most common cryptographic techniques for signing JWTs are:

• HMAC (Hash-based Message Authentication Code) is a symmetric algorithm that uses a hash function and a secret key to both sign and verify the token.
• RSA (Rivest-Shamir-Adleman) is an asymmetric algorithm that uses a public and private key pair to generate and verify a signature.
• ECDSA (Elliptic Curve Digital Signature Algorithm) is also an asymmetric algorithm that uses a public and private key pair but is based on elliptic curve cryptography, offering faster performance and smaller key sizes compared to RSA.

In the next sections, we’ll examine HMAC, RSA, and ECDSA in more detail and help you determine which algorithm is best suited for your needs.

HMAC and HS256

HMAC provides a way to verify the integrity and authenticity of a message by combining a hash function with a secret key.

1. First, you have a message (e.g., a JWT) and a secret key that only the sender and receiver know.
2. You use a hash function (like SHA-256) to process the message and the secret key together. The hash function takes the message and key and creates a fixed-size "fingerprint" (a hash) of the combination.
3. This "fingerprint" is the HMAC. It’s a unique value based on both the content of the message and the secret key.
4. When the receiver gets the message, they can create the HMAC using the same hash function and secret key. If their result matches the HMAC you sent, they know that:
   • The message hasn’t been tampered with (integrity).
   • The sender knows the secret key, so the message is authentic.

The HMAC family contains more than one algorithm, with the difference being the size of the hash (the bigger the hash, the more secure it is):

• HS256: HMAC with SHA-256, the most commonly used option for signing JWTs.
• HS384: HMAC with SHA-384 (a larger hash size).
• HS512: HMAC with SHA-512 (even larger hash size).

!!SHA-256 is part of the SHA-2 family of cryptographic hash functions. It generates a fixed-length (256-bit) hash value from the input data. This hash is computationally infeasible to reverse (pre-image resistance) and collision-resistant, meaning it's highly unlikely to find two different inputs that produce the same hash.!!

In the HS256 algorithm:

1. A message (or data) is hashed using the SHA-256 algorithm.
2. The hash is then combined with a secret key using the HMAC process.
3. The result is a 256-bit signature that uniquely represents the message and the secret key combination.

In practice, this is how you would use HS256 to create and verify a JWT with Python:

  
import hmac
import hashlib
import base64
import json

# Function to encode data in base64 (url-safe)
def base64_url_encode(data):
    return base64.urlsafe_b64encode(data).rstrip(b'=')

# Function to create the HMAC-SHA256 signature
def create_hmac_signature(data, secret_key):
    return hmac.new(secret_key.encode(), data.encode(), hashlib.sha256).digest()

# Function to create a simple JWT-like token
def create_jwt(payload, secret_key):
    # Step 1: Encode the header
    header = {
        "alg": "HS256",
        "typ": "JWT"
    }
    header_encoded = base64_url_encode(json.dumps(header).encode())

    # Step 2: Encode the payload (the message)
    payload_encoded = base64_url_encode(json.dumps(payload).encode())

    # Step 3: Create the signature
    message = header_encoded + b'.' + payload_encoded
    signature = create_hmac_signature(message.decode(), secret_key)
    signature_encoded = base64_url_encode(signature)

    # Combine header, payload, and signature to create the JWT
    jwt_token = header_encoded + b'.' + payload_encoded + b'.' + signature_encoded
    return jwt_token.decode()

# Function to verify the HMAC-SHA256 signature
def verify_jwt(jwt_token, secret_key):
    # Split the token into header, payload, and signature
    parts = jwt_token.split('.')
    if len(parts) != 3:
        return False
    
    header_encoded, payload_encoded, signature_encoded = parts

    # Recreate the message from header and payload
    message = header_encoded + b'.' + payload_encoded

    # Create a signature using the secret key
    expected_signature = create_hmac_signature(message.decode(), secret_key)
    expected_signature_encoded = base64_url_encode(expected_signature)

    # Compare the expected signature with the one provided in the token
    return signature_encoded == expected_signature_encoded.decode()

# Example usage
secret_key = "mysecretkey"

# Example payload (could be any data you want to send)
payload = {
    "user": "john_doe",
    "role": "admin"
}

# Create the JWT token
jwt_token = create_jwt(payload, secret_key)
print("Generated JWT:", jwt_token)

# Verify the JWT token
is_valid = verify_jwt(jwt_token, secret_key)
print("Is the token valid?", is_valid)
  

The code does the following:

1. Generates a header and a payload: {"user": "john_doe", "role": "admin"}.
2. Uses HMAC with SHA-256 to create a signature and combine everything to create the token.
3. Verifies the token by checking if the signature matches the one we created using the same secret key.

RSA and RS256

RSA stands for Rivest-Shamir-Adleman, and it’s an asymmetric public-key cryptosystem. What does that mean?

Asymmetric means that two different keys are used: one for encryption and a different one for decryption. These keys are known as the public key and the private key.

• The public key is shared with everyone. People use it to verify or encrypt messages that only the owner of the matching private key can decrypt.
• The private key is kept secret by the owner. It is used to sign or decrypt messages that were encrypted with the matching public key.

Something important to understand about RSA is that it can be used both for encryption and signing, depending on how the keys are used:

• To use RSA for encryption, the message must be signed with the recipient’s public key. This means that the message can only be decrypted by the private key, ensuring that only the recipient can read it.
• To use RSA for signing a message, you use your private key. This creates a digital signature that proves that the message is authentic and hasn't been tampered with. Anyone with your public key can verify the signature to ensure it's really from you and that the message is intact.

When we talk about RSA in the context of JWTs, it’s almost always about signing the token. RSA can be used for both signing and encryption, but for JWTs, it's typically used in the context of signing.

Here is how RSA works:

1. First, we generate the RSA key pair. The private key (which should be kept secure and private) is used to sign the JWT. The public key is used by recipients to verify the JWT’s signature (this key can be shared). Here is how these keys are generated:
   1. First, two large prime numbers are selected.
   2. These primes are multiplied together to create a modulus, which is part of both the public key and private key.
   3. A public key exponent and a private key exponent are then generated, which are mathematically related but hard to compute without knowing the private key.
2. When the JWT is created, its header must specify the signing algorithm (e.g., RS256). Both the header and payload are Base64Url encoded.
3. A hash (SHA-256, for example) of the header and payload is created.
4. The hash is then signed using the private RSA key to create a signature.
5. The JWT is created by concatenating:
   1. The Base64Url-encoded header
   2. The Base64Url-encoded payload
   3. The signature (the RSA signature of the header and payload)
6. When the recipient receives the JWT, it splits it into the header, payload, and signature.
7. The recipient then recomputes the hash of the header and payload (same way the sender did).
8. The recipient uses the public RSA key to verify the signature. If the signature matches the recomputed hash, the JWT is valid and the data is considered authentic and unaltered.

The security of RSA is based on the difficulty of factoring large numbers. While it's easy to multiply two large primes together, it's computationally infeasible to factorize their product back into the original primes, especially as the number size grows.

RS256 combines RSA with SHA-256, a cryptographic hash function that takes some input (like a message) and creates a fixed-size, unique output (a hash). In RS256, this hash is used to ensure the integrity of the data before it’s signed with the private key.

Here is how it works:

1. First, the data (like a JWT) is hashed using SHA-256 to create a fixed-length hash.
2. Then, the RSA private key is used to sign this hash, creating a signature.
3. To verify the signature, anyone with the matching RSA public key can check the signature against the data and make sure it hasn't been tampered with.

In practice, this is how you would use RS256 to create and verify a JWT with Python:

  
import jwt
import rsa
from datetime import datetime, timedelta

# Step 1: Generate an RSA key pair (private and public keys)
private_key, public_key = rsa.newkeys(2048)  # Using 2048 bits for stronger security

# Step 2: Create a JWT payload
payload = {
    "sub": "1234567890",  # Subject (could be user ID or similar)
    "name": "John Doe",
    "iat": datetime.utcnow(),  # Issued at time
    "exp": datetime.utcnow() + timedelta(hours=1)  # Expiration time (1 hour from now)
}

# Step 3: Sign the JWT with the private key using RS256 algorithm
encoded_jwt = jwt.encode(payload, private_key, algorithm="RS256")

print("Encoded JWT (signed):", encoded_jwt)

# Step 4: Verify the JWT with the public key
try:
    decoded_jwt = jwt.decode(encoded_jwt, public_key, algorithms=["RS256"])
    print("Decoded JWT:", decoded_jwt)
except jwt.ExpiredSignatureError:
    print("Token has expired")
except jwt.InvalidTokenError:
    print("Invalid token")
  

The code does the following:

1. Generate a 2048-bit RSA key pair using rsa.newkeys(2048).
2. The payload is a dictionary containing standard JWT claims like sub (subject), iat (issued at), and exp (expiration time).
3. We use the jwt.encode() function from the PyJWT  library to sign the payload. The private_key is used to sign the token with the RS256 algorithm.
4. To verify, we use the jwt.decode() function, which takes the signed JWT, the public_key, and the algorithm used (RS256 in this case). If the JWT is valid and the signature matches, it will return the decoded payload. If the signature doesn't match or the token is expired, it will raise an error.

What about RSASSA-PSS?

RSASSA-PSS (Probabilistic Signature Scheme) is technically more secure than RS256 (RSA with SHA-256), but whether it is better for JWT signing depends on the specific requirements and trade-offs of your use case.

• RSASSA-PSS is more secure: RSASSA-PSS uses random padding (a salt), which makes it more resistant to certain types of cryptographic attacks, such as chosen-message attacks and signature malleability. This provides better resilience against potential weaknesses in deterministic signature schemes. On the other hand, RS256 is deterministic (always produces the same signature for the same input). While this makes it easier to implement and use, it can be vulnerable to certain attacks if the private key is compromised multiple times with the same message. So while RS256 is still considered secure, it’s less secure than RSASSA-PSS due to the lack of randomness in the padding process.
• RSASSA-PSS is slower: RSASSA-PSS typically has a slightly higher computational overhead due to the additional randomness in the padding process, especially during signing. However, this overhead is generally minimal and may not be noticeable unless you are signing large volumes of tokens.
• RS256 is more widely adopted: RS256 is very widely supported and is the default in many JWT libraries and systems, making it highly compatible with existing applications. RSASSA-PSS is more modern and recommended for high-security environments, but it might not be as universally supported or compatible with all systems that expect RS256.

If security is your top priority and you can handle the additional overhead and possible compatibility concerns, RSASSA-PSS is a better option. If compatibility and performance are more important, RS256 is still a strong choice and is widely used in production systems.

ECDSA and ES256

ECDSA is an asymmetric digital signature algorithm based on Elliptic Curve Cryptography (ECC). It offers the same level of security as other traditional algorithms (e.g., RSA) but with smaller key sizes, making it more efficient in terms of performance and storage.

ECDSA works by generating a private key and public key. The private key signs the message, and the public key is used by others to verify that the signature is valid.

ES256 is a specific implementation of ECDSA used for JWT signing. It uses:

• The P-256 elliptic curve, which is a curve defined by the NIST (National Institute of Standards and Technology) for use in elliptic curve cryptography. P-256 (also known as secp256r1) is a 256-bit curve and is widely used in security protocols like TLS and SSL for secure communication.
• The SHA-256 hashing algorithm to create a fixed-size digest of the message before signing it.

ES256 provides a strong level of security using a 256-bit key size, which is considered secure for most use cases, offering similar security strength as 3072-bit RSA. It is considered efficient in terms of speed and memory usage, particularly on resource-constrained devices or systems with limited computing power.

Here is how ES256 works:

1. First, the private and public keys are generated using the P-256 elliptic curve:
   • The private key is a randomly generated secret key (an integer).
   • The public key is derived from the private key, using elliptic curve mathematics.
2. When the JWT is created, its header must specify the signing algorithm (e.g., ES256). Both the header and payload are Base64Url encoded.
3. Before signing, the concatenated header + payload is passed through the SHA-256 hash function. This generates a 256-bit hash (a fixed-length digest) of the data. This hash is used as the message to be signed: SHA-256(header + "." + payload)
4. The private key is used to sign the hash. The signing process is the core part of ECDSA and involves elliptic curve math. Specifically, it involves:
   • Generating a random integer (k).
   • Calculating an elliptic curve point, called R, based on the random integer (k) and the curve's properties.
   • Using the private key and the curve's properties to compute a signature. The signature consists of two components:
     • r: An x-coordinate from the elliptic curve point R.
     • s: A value derived from the private key, the hash of the data, and the random integer k.
5. The signature is represented as a pair of values (r, s), which are then Base64Url-encoded to form the signature part of the JWT.
6. The final JWT is created by concatenating the Base64Url-encoded header, payload, and signature, separated by full stops: Base64Url(header) + "." + Base64Url(payload) + "." + Base64Url(signature)‍
7. When the recipient receives the JWT, they take the header and payload and reconstruct the same data that was used during signing (Base64Url-encoded and concatenated).
8. The recipient applies SHA-256 to the concatenated header + payload to compute the hash of the data:
9. Using the public key, the recipient can verify the signature using elliptic curve mathematics:
   • They will check whether the signature (r, s) is valid for the computed hash.
   • The public key is used in the verification equation, which checks if the elliptic curve signature matches the hash of the data.
10. If the signature is valid, the data has not been tampered with and the JWT is considered authentic.

Let’s see how you would use ES256 to create and verify a JWT with Python. You’ll need the following Python libraries:

• PyJWT for handling JWT creation and validation.
• cryptography for generating the elliptic curve keys (P-256).

  
import jwt
from cryptography.hazmat.primitives.asymmetric import ec
from cryptography.hazmat.primitives import hashes
from cryptography.hazmat.primitives.asymmetric import padding
from cryptography.hazmat.primitives import serialization
from datetime import datetime, timedelta

# Step 1: Generate the private and public keys using P-256 curve
private_key = ec.generate_private_key(ec.SECP256R1())  # Generate a private key using P-256 (SECP256R1)
public_key = private_key.public_key()  # Generate the corresponding public key

# Step 2: Create a JWT payload
payload = {
    "sub": "1234567890",  # Subject (could be a user ID or similar)
    "name": "John Doe",
    "iat": datetime.utcnow(),  # Issued at time
    "exp": datetime.utcnow() + timedelta(hours=1)  # Expiration time (1 hour from now)
}

# Step 3: Sign the JWT with the private key (using ES256)
encoded_jwt = jwt.encode(payload, private_key, algorithm="ES256")

print("Encoded JWT (signed):", encoded_jwt)

# Step 4: Verify the JWT with the public key
try:
    decoded_jwt = jwt.decode(encoded_jwt, public_key, algorithms=["ES256"])
    print("Decoded JWT:", decoded_jwt)
except jwt.ExpiredSignatureError:
    print("Token has expired")
except jwt.InvalidTokenError:
    print("Invalid token")
  

The code does the following:

• We generate a private key using the P-256 elliptic curve (SECP256R1) through the cryptography library. The public key is then derived from the private key.
• We create a sample payload that contains standard JWT claims like sub (subject), name (user's name), iat (issued at), and exp (expiration time).
• We use jwt.encode() from the PyJWT library to sign the JWT. We pass the private key and specify the ES256 algorithm to sign the JWT.
• On the receiving end, we use jwt.decode() to verify the JWT. The public key is used to validate the signature. If the JWT is valid, the decoded payload is returned.

What about EdDSA?

EdDSA (Edwards-curve Digital Signature Algorithm) is generally considered better than ECDSA for most use cases. It’s a type of elliptic curve cryptography that utilizes twisted Edwards curves. It is based on Schnorr's signature scheme, rather than DSA. EdDSA is efficient for both signing and verification, produces compact signatures, and avoids many common security vulnerabilities:

• EdDSA always generates the same signature for the same message, reducing the risk of vulnerabilities related to weak random number generation, which has been a known issue with ECDSA (where improper randomness in generating the k value could allow attackers to recover the private key).
• EdDSA uses the Ed25519 curve, which has been specifically designed to be resistant to various cryptographic attacks, including side-channel attacks. The curve parameters and implementation details are chosen to provide strong security with minimal room for implementation flaws.
• EdDSA generally provides faster signing and verification compared to ECDSA. ECDSA can be slower in comparison, particularly for higher security levels (larger key sizes). EdDSA (with Ed25519) offers comparable security to ECDSA with a 256-bit key but with significantly better performance.
• EdDSA is easier and less error-prone to implement than ECDSA. Its deterministic nature means you don't need to worry about weak randomness, which is one of the common sources of mistakes in ECDSA implementations (mistakes in randomness can lead to serious vulnerabilities, such as the leakage of private keys).

EdDSA has seen growing adoption in modern cryptographic protocols, including SSH, OpenPGP, and TLS, because of its stronger security properties and efficiency. ECDSA is widely used and still supported, especially in blockchain technologies like Bitcoin and Ethereum, but its implementation challenges and performance limitations have led to the increasing preference for EdDSA in new systems.

To sum up, EdDSA is faster, more secure, and easier to implement than ECDSA. If you choose to use elliptic curve cryptography to sign your tokens, go for EdDSA if possible.

Here is a Python example for signing and verifying JWTs using EdDSA:

  
import jwt
from cryptography.hazmat.primitives.asymmetric import ed25519

# Generate a private key (Ed25519)
private_key = ed25519.Ed25519PrivateKey.generate()

# Derive the corresponding public key
public_key = private_key.public_key()

# Create a payload for the JWT
payload = {"user": "example_user", "role": "admin"}

# Sign the JWT with the private key using EdDSA (Ed25519)
encoded_jwt = jwt.encode(payload, private_key, algorithm="EdDSA")

print("Signed JWT:", encoded_jwt)

# To verify the JWT, use the public key
try:
    decoded_jwt = jwt.decode(encoded_jwt, public_key, algorithms=["EdDSA"])
    print("Decoded JWT:", decoded_jwt)
except jwt.ExpiredSignatureError:
    print("JWT has expired")
except jwt.InvalidTokenError:
    print("Invalid token")
  

The PyJWT library supports EdDSA (specifically Ed25519) for signing and verifying JWTs as of version 2.0.0.

What size of hash should you use?

The level of security each cryptographic hash function provides is roughly half of its output size. So SHA-256 gives you about 128 bits of security since it produces a 256-bit hash, while SHA-512 offers about 256 bits of security because of its 512-bit output. This means that an attacker would need to generate around 2^128 hashes before they could start finding collisions, thanks to the birthday paradox.

!!The birthday paradox refers to the counterintuitive probability that in a group of just 23 people, there's a better-than-even chance that two of them share the same birthday. In the context of cryptography, it means that finding two different inputs (like messages) that produce the same hash (a collision) is easier than you'd think, even with a large hash space. The probability of finding a collision increases much faster than you'd expect as the number of possibilities grows, which is why we consider 128-bits of security sufficient—because you don't need to try all possible values to find a match.!!

In practice, SHA-256 is strong and secure enough for almost anything you’ll need in the near future. You really won’t need anything stronger anytime soon. The key takeaway here is to stay away from older, less secure algorithms like SHA-1, which has known vulnerabilities and should be avoided for any serious use.

To sum up, for solid security, aim for at least 128-bit protection and stick with modern options like SHA-256. Avoid SHA-1 at all costs.

The bottom line: Which algorithm should you use?

As always, the answer to this question is: it depends.

Are you building an internal app or a microservices system where multiple clients must sign and verify JWTs?

What are your security requirements?

Are you building a high-throughput system that will be signing a lot of tokens, and you need to optimize for this?

Are you building for mobile or IoT devices?

Is performance and security absolutely crucial for your app?

• If you're working with microservices, distributed systems, or public APIs where JWTs need to be securely shared and verified without exposing secrets, RS256 is a safe and popular choice. It's widely used in scenarios like OAuth 2.0, OpenID Connect, and other authentication protocols where asymmetric key cryptography is needed for signing and verifying JWTs.
• If performance is a concern, or you're building for mobile apps or constrained devices, ES256 offers a good balance of security and efficiency and is becoming more popular in modern applications every day. It is highly recommended, especially when working with mobile devices or environments where performance and security are both crucial. If possible, go for EdDSA instead of ECDSA. It's faster, more secure, and easier to implement.
• If your use case is internal and you control both the signing and verification process (i.e., you're not sharing the public key), HS256 can be a fast and simple choice. In general, using HMAC to sign tokens is considered an anti-pattern for several reasons, so if you find yourself in this position, think about whether JWTs is the right choice for you. Remember that if you use HMAC to sign JWTs, every service or entity that needs to verify the token must have access to the same secret key. This introduces key distribution and key management problems, especially as the number of services grows in a microservices architecture. If one service is compromised and the secret key is leaked, all services relying on that key are vulnerable. It’s a well-established best practice to use asymmetric algorithms like RS256, ES256, or EdDSA for JWT signing.

RSA vs. ECDSA

Some people prefer RSA than ECDSA for JWT signing because JWTs are signed once and verified many times; thus, RSA is more appropriate because it's slower to sign and faster to verify. While this statement is true (due to its public-key verification process RSA verifies tokens faster than ECDSA), deciding which one to use depends on other factors as well.

For example, if you are building a high-throughput system, then RSA's signing speed disadvantage becomes noticeable if you need to sign a lot of tokens.

Also, for JWTs, where the signing happens once (e.g., by an authorization server) and the verification happens multiple times (e.g., by clients or services), the signing process's speed is often more important than verification speed.

While RSA might offer faster verification, ECDSA is typically a better choice for signing JWTs because it is more efficient for signing and provides strong security with smaller key sizes (a short elliptic curve key of around 256 bits provides the same security as a 3072 bit RSA key).

However, before making your choice, remember that while ES256 is becoming increasingly popular, RSA-based signatures remain the default or required choice for certain standards (OAuth 2.0, OIDC, SAML, X.509 certificates, JWS, etc.) due to their long-standing use and wide compatibility.

In some government and regulatory standards, RSA-based signatures are explicitly required, as RSA has been a standard for digital signatures for many years. For example, some standards developed by NIST may emphasize RSA for specific use cases like digital signatures in e-government applications. Before going for ES256, ensure that it’s a viable option for your business.